Assignment 5: Java and TileLand
solution- This assignment shows the power of numeric variables and loops for complex tasks like making tile patterns.
- Part A Repetition
-
In the Java world, we will be examining for-loops and a method call. In the Tileland world a loop of triangles with a number of square spacers.
- Examine PLoop.java. To have the output of this program inserted into
Tileland we must sneak it into an existing TileLand program. Go to TileLand
and click "new" then the nearby "<". Now view the W:\cs216\TestTLFiles by
"modified" (so that the latest file will be easy to find at the bottom).
Open the latest file with wordPad and insert the output of your program into i
program[""]
so that it reads
program["triangle blue triangle blue triangle blue triangle blue triangle blue triangle blue "]
now click the ">" and you will be able to see the results of your cutting and pasting into TileLand. If you also stick some text into comment[""] like comment["java"], then you will also be able to more easily verify you are looking at the right changes. - write a method called spacer that takes an integer parameter and a String like "orange " but returns nothing. The method will instead print to the screen "square orange " a number of times. In fact the number of times should be same number as the int parmeter. So spacer will be able to create an number of squares of a specified colour.
- Between each "triangle blue " have java call the spacer method. Show the text output for calls where 0, 1, 2, 4, and 8 are used as the parameter for spacer. Underline the "triangle blue " through out the output. Test to make sure that each of the text outputs work in TileLand. If a parameter doesn't work, explain why not.
File content not available for PLoop.java
- Examine PLoop.java. To have the output of this program inserted into
Tileland we must sneak it into an existing TileLand program. Go to TileLand
and click "new" then the nearby "<". Now view the W:\cs216\TestTLFiles by
"modified" (so that the latest file will be easy to find at the bottom).
Open the latest file with wordPad and insert the output of your program into i
- Modify your program from part A to generate the follow spirals. Think about having a increasing number spacers.
- Why does the center square of the last three patterns mess up the number pattern of the differently coloured squares? In the program, how can the first square be created?
- In theory, all of the spiral programs from PolygonR&D can be rewritten into Java programs. Explain why PolygonR&D's expand type (see Code5.java) programs would be not as easy to translate.
Assignment 4: String along with me
- This assignment examines Strings and basic Java programming with variables.
- Part A Playing with Strings
- Examine StringOne.java below and answer the following questions.
- Create method calls that will produce
- "a cow likes jim but not a cow."
- "She likes him but not his friends."
- " likes but not ."
- Create new methods that will produce sentences of this form. (# is a value and _____ is a blank for a variable
- "My _____ is ______ and ______."
- "_____ has # dollars in one pocket and # in another, and so # in total."
- "# times # plus # equals #."
File content not available for StringOne.java
- Create method calls that will produce
File content not available for BinaryStr.java
- Consider the code BinaryStr.java.
- What is the signature for the method convertBinary?
- How is the "/" different from division? Give a concrete example.
- What is 2008 in binary?
- Write a new method called convertTernary that converts base 10 numbers into base 3 numbers. Convert 2008 into base 3.
- Include the following method in your code.
File content not available for readBinary.java
- What is the signature for the method convertBinary?
- Write a line in the main that calls this method that converts 110001101.
- What happens with the call readBinary("1aaa1"),readBinary("12021"), and readBinary("110 ")? How does the method interpret the a's, spaces, and 2's?
- Rewrite readBinary so that it ignores spaces and yet correctly computes the binary value.
- Write a new method called readTernary that converts base 3 numbers into base 10 numbers. Convert 120121 into base 10.
Assignment 3: coding algorithms
Solution- This assignment examines programming (coding) with algorithms in PolygonR&D. Some algorithms can make patterns others can do computations.
- Part A making patterns
There is more than one algorithm to create a zig-zag tile pattern,
as well as more than one way to code it.
- Examine the code Oct1 and Oct2 (below).
- What do they do? Why are they considered zig-zag patterns?
- Which one is the most efficient in term of number of instructions? Explain.
- Which program contains more semantic information? Explain.
- In Oct2, modify path and pathBack to create the pattern in the figure
below. Explain the relationship between path and pathBack.

- Modify path and pathBack to create your own interesting pattern.
File content not available for Oct1.java
File content not available for Oct2.java
- Examine the code Oct3.
File content not available for Oct3.java
- Which program has the fewer lines of code Oct3 or Oct2?
- For the same area of the pattern which uses more paints?
- How does Oct3 differ from the standard expand program?
- How difficult is it to create your interesting pattern using Oct3's algorithm?
- Write a program based on Oct3 that uses triangles instead of octagons for the basis of the pattern.
- Examine the code Oct1 and Oct2 (below).
- Part B computations
- Low-level computations on a computer are achieved by using binary: ones and zeros. In PolygonR&D, similar computations can be achieved by using coloured squares. This means that we will interpret squares colours as having a numeric value. We will examine ways of representing numbers as uniary (tallies --like base 1) and as binary (base 2).
- Examine the code UniAdd.
File content not available for UniAdd.java
- Insert comments into the UniAdd codes so that the meaning / purpose of the code is clearer.
- How many ifs in total are used to add 111 with 111?
- Sometimes the random numbers are too big or too small to be interesting. Convert the code so that the numbers to be added are more than 2 and less than 8.
- Translate the code so that the sum displays in binary.
- Rewrite rNum so that it creates random binary numbers between 4 and 32.
- Rewrite AddNum and it's subprograms so that it correctly adds binary numbers.
- Rewrite AddNum so it adds column-wise.
- Compare the ifs used during the addition of 111 with 111 for each of the binary AddNums (non-columns and column-wise).
- What are the biggest number that can be added (without changing the program with scaling etc) in the original UniAdd and the binary version of the code? What if ternary (base 3) was used instead?
- Hints.... look at the old assignment 3.
Assignment 2: describing algorithms
- This assignment examines algorithms that rely on conditional behavior. Previous algorithms that dealt with elaborating an existing loop by inserting spacers or interleaving a zig-zag of odd-sided polygons implicitly contained a condition--stop if you have completed the loop. In these new algorithms the conditions serve a more important role; they determine how the pattern develops.
- Part A

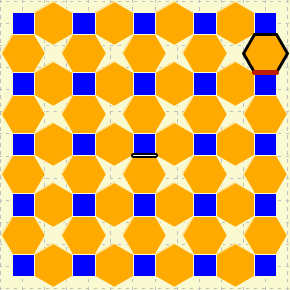 Consider these two different ways for creating this pattern in Tileland:
Consider these two different ways for creating this pattern in Tileland:
- have the building block be "hexagon orange square blue turn"
- have the building block be "square blue turn hexagon orange"
- Use each of the building blocks to create the pattern.
- Questions
- Identify the grid and the spacers for each pattern.
- Describe in words the algorithms that you need to use for each building block.
- Describe with pictures in a diagram the algorithms that you need to use for each building block.
- Which of the methods of is more efficient for this pattern?
- The focus on the spacers or the grid tiles is different. Since neither the spacers nor the grid is complex, the pattern is not difficult to construct.
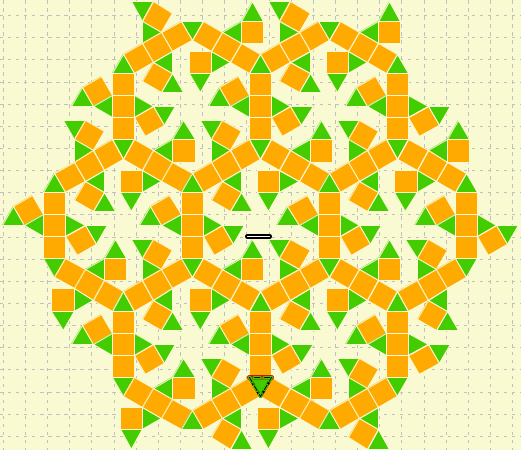
 For these patterns, use only one (the most efficient one) of the algorithms to construct these patterns.
For these patterns, use only one (the most efficient one) of the algorithms to construct these patterns.
- More Questions
- Describe with pictures in a diagram the algorithms that you used to make these patterns.
- For each pattern, what is the better focus for the constructions. Why?
- Part B
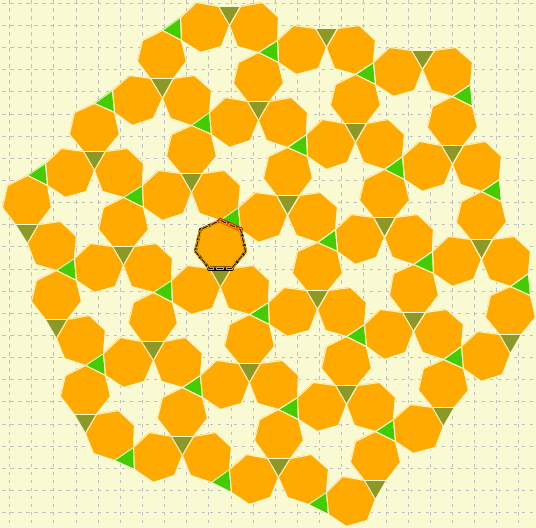 Create this pattern and pay particular attention to how you construct it. It may require you to make it many times and perhaps a few different ways: in particular make sure that you use one that relies on cutting and pasting.
Create this pattern and pay particular attention to how you construct it. It may require you to make it many times and perhaps a few different ways: in particular make sure that you use one that relies on cutting and pasting.
- Questions
- Describe how the algorithm you used to construct this pattern. What made this pattern more difficult than the above patterns?
- Explicitly write down a sequence of character that will construct this pattern. For example, a sequence of letters that creates a square grid is :
4 r t a x v v v v v t v v v v t v v v v t v v v t v v v v t v v v t v v v v t v v v t v v v t v v v v t v v v t v v v t v v v v t v v v t v v v t v v v t v v v v t v v v t v v v t v v v t v v v v t v v v t v v v t v v v t v v v t v v v v t v v v t v v v t v v v t v v v t v v v v t ...
Be wary--this is a difficult task.
Assignment 1: making polygon loops and stars
- This assignment examines algorithms and their effectiveness. An algorithm has a number attributes that are interesting: correctness, efficiency, and simplicity.
- Part A
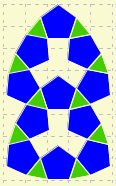 Consider at least two different ways for creating this pattern in Tileland.
Consider at least two different ways for creating this pattern in Tileland.
- Questions
- Describe two ways that you created the pattern using words, then try to describe it using diagrams with arrows.
- Compare the twos way that you made the pattern in terms of correctness, efficiency, and simplicity.
- Write up a definition for algorithm (state your resource).
- Part B
-

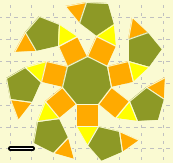
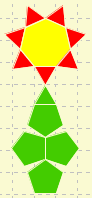
- Questions
- What are the minimum number of instructions to create these patterns in TileLand? Describe the method you used to construct these pattern.
- What is the minimum number of mouse clicks?
- Create your own interesting repetitive pattern that does not require a lot of clicks but has a lot of instructions. What makes the pattern interesting?
-



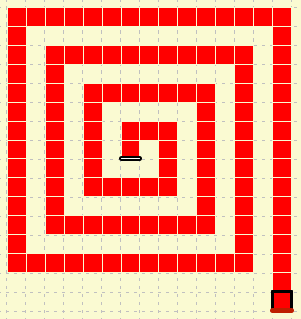
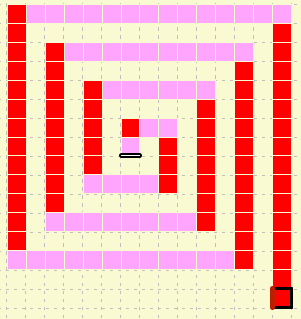

 Formating of this page is based on resources from
Formating of this page is based on resources from